INTRODUÇÃO

Pitágoras de Samos foi um dos grandes pensadores da Antiguidade, tanto como matemático, como filósofo e líder espiritual. Fundou a escola pitagórica, e influenciou a matemática e filosofia, defendendo que a matemática é a entrada para compreender o universo e os números base de todas as coisas (Tomaz, 2019). Pitágoras enxergava a harmonia como princípio universal. Ele foi pioneiro na compreensão que os números estavam no centro da existência, e os pensamentos sobre matemática influenciaram no progresso o da geometria, da música e da filosofia (Silva, 2022). Contudo, o teorema diz que “em um triângulo retângulo, a área do quadrado construída sobre a hipotenusa é igual à soma das áreas dos quadrados construídos sobre os catetos”. 

Pitágoras fundou a comunidade filosófica e religiosa conhecida como a Escola Pitagórica, com a narrativa que o universo poderia ser explicado por vários números e projeções matemáticas. A escola pitagórica era um encontro de estudos com regras. Pitágoras acreditava que o saber e compreensão sobre a realidade poderiam ser atingidos mediante a matemática, espírito e razão (Magalhães, 2023).

O Teorema de Pitágoras é na atualidade uma das contribuições mais longas à matemática. O teorema afirma que um triângulo retângulo e o quadrado da hipotenusa, o lado oposto ao ângulo reto, é igual à soma dos quadrados dos outros dois lados, vejamos: a^2+b^2 = c^2. Contudo, significa que a e b são os catetos e c é a hipotenusa. Esse entendimento na geometria é uma referência para a evolução da matemática, aplicado em várias áreas, como, engenharia, astronomia e arquitetura (Oliveira, 2021). Pitágoras não foi o único a encontrar esse teorema, contudo, a escola fundada por ele, adotou e implementou o teorema em suas bases filosóficas, comunicando como uma das bases da educação matemática na época (Fossa, 2021).

O legado deixado por Pitágoras vai além dos seus achados matemáticos. Sua filosofia, tinha relação com a matemática, espiritualidade e a harmonia, sendo influenciado pela filosofia ocidental, em escolas baseadas em Platão, um dos filósofos mais influentes da Grécia antiga, e estóica, composta por Marco Aurélio e Sêneca. Pitágoras foi fonte de inspiração para outros pensadores e matemáticos, como, por exemplo, Platão, Aristóteles, Euclides, entre outros, que exploravam a matemática e a filosofia (Paiva, 2021).

Resta claro a relevância do Teorema de Pitágoras para o desenvolvimento da Matemática, no passado e presente. A aplicabilidade de triângulos retângulos, esclarece as relações entre as dimensões e seus lados, oportunizando solidez na resolução de problemas geométricos e trigonométricos. Afirma-se que o Teorema de Pitágoras é fundamental em ciências exatas sendo indispensável para qualquer estudante ou profissional que almeje compreender o imenso universo matemático (Silva; Burmann 2023).

Neste artigo, serão abordadas algumas contribuições de Pitágoras e descobertas matemáticas e filosóficas. Esse teorema é útil para a geometria e cotidiano, tendo em vista, suas aplicações surgirem com frequência. Ressalta-se que, até o momento, os escritos originais não foram vistos, assim, não é possível asseverar com toda a certeza, que Pitágoras prova sobre o teorema que possui seu nome (Alves, 2024).

A pesquisa foi realizada com abordagem bibliográfica, em um processo sistemático de busca e análise de informações e conhecimentos já existentes em livros, artigos, teses, dissertações e outros materiais bibliográficos, para fornecer análise crítica sobre os melhores resultados. Para a escolha dos documentos, realizou-se pesquisa na internet, em bases de dados. Foram delimitados os seguintes critérios de inclusão, artigos nacionais, dos últimos 6 anos, disponíveis gratuita e integralmente, publicados entre 2018 até 2024. Além da análise de artigos. O artigo possui relevância para a sociedade acadêmica e contemporânea, pois, a temática oportuniza conhecimento ao indivíduo que pretende conhecer mais sobre o teorema e o filósofo estudado neste artigo. 

O artigo foi subdividido em seções, iniciando com a relação fundamental em triângulos retângulos, que afirma que o quadrado da hipotenusa é igual à soma dos quadrados dos catetos; em seguida, foram apresentados os números figurados, que podem ser representados por figuras geométricas, como números triangulares, quadrados e pentagonais. Por fim, traz algumas explicações sobre os números perfeitos, identificados como números que são iguais à soma de seus divisores próprios, como 6 e 28.  

OBJETIVOS

• Auxiliar às pessoas interessadas em conhecer sobre este teorema e suas aplicações em diversas áreas do conhecimento;
• Analisar algumas descobertas relacionadas ao Teorema de Pitágoras;
• Demonstrar como o Teorema de Pitágoras pode ser ferramenta indispensável para compreender e solucionar questões do cotidiano, facilitando a interação e evidenciar a transformação que proporcionou para sociedade com novas características e soluções de problemas.

PROBLEMÁTICA

A problemática versa sobre a contribuição do Teorema de Pitágoras na sociedade atual. Como podemos utilizar esse teorema em nosso cotidiano? E como o teorema impacta positivamente a atualidade mediante as suas funções e aplicabilidade? Observou-se escassez de revistas e artigos científicos que versem sobre a temática, ou seja, a filosofia antiga, sendo mais direcionada ao campo da matemática, resta evidente, que a forma como Pitágoras de Samos contribuiu/contribui para ciência contemporânea, é o objetivo do referido artigo.

JUSTIFICATIVA

A temática justifica-se por compreender que o Teorema de Pitágoras contribui de forma positiva para a sociedade atual mediante as suas funções. A pesquisa obtém possíveis respostas para alguns questionamentos sobre o Teorema de Pitágoras de Samos e algumas de suas descobertas, que existem na sociedade contemporânea, dentre as quais, destaca-se a contribuição para a ciência pós-moderna, buscando, demonstrar a importância deste grande filósofo e pesquisador para atualidade.

FUNDAMENTAÇÃO TEÓRICO-METODOLÓGICA DA INVESTIGAÇÃO

Para os pitagóricos, a matemática não era apenas um instrumento prático, o Teorema de Pitágoras não foi apenas uma descoberta geométrica, significava uma relação intensa entre os números e o mundo físico (Paiva, 2021). A contribuição de Pitágoras foi modificar o conhecimento prático em um teorema matemático. Ele demonstrou, diante a matemática, que a soma dos quadrados dos catetos é sempre igual ao quadrado da hipotenusa, independentemente das medidas determinadas dos lados (Rabelo, 2021). 

O Teorema de Pitágoras conceituada por Cintra e Cintra (2003 apud Magalhães, 2020) define: “A área do quadrado cujo lado é a hipotenusa de um triângulo retângulo for igual à soma das áreas dos quadrados cujos lados são cada um dos catetos desse mesmo triângulo.”

A determinada fórmula é bem conhecida e aplicada em matemática. Ela é usada em vários campos da ciência e da engenharia, além de escolas que utilizam a geometria. O fundamento do teorema está na relação entre os lados de um triângulo retângulo, onde a soma dos quadrados dos dois lados menores, os catetos, resulta sempre igual ao quadrado do lado maior, a hipotenusa (Asth, 2021). 

Embora o teorema possua alguns limites diante sua aplicabilidade, sua importância permanece baseada na geometria, e seu suporte pode ser identificado em outras fundamentações avançadas. O Teorema de Pitágoras é norteador da matemática e função vai além da sala de aula. Desde sua origem, o teorema continua ser instrumento essencial para resolver problemas geométricos e calcular distâncias, mesmo sendo simples, é poderoso, é uma evidência de como a matemática é útil em várias situações diárias 

Desta forma, a comprovação de um teorema significa a sua validade, ou seja, é a sequência de argumentos matemáticos que afirmam a aplicação do teorema. No caso do teorema de Pitágoras, existem várias demonstrações (Silva; Burmann 2023). Conhecer de fato as medidas dos triângulos é uma das estratégias para encontrar de maneira rápida um dos lados de um triângulo retângulo. O teorema de Pitágoras não define a relação entre ângulos de um triângulo retângulo, e sim entre lados de um triângulo retângulo.

TEOREMA DE PITÁGORAS

Mesmo compreendendo que a identificação do teorema esteja associado ao filósofo e matemático grego Pitágoras, é essencial perceber que a compreensão sobre a relação entre os lados de um triângulo retângulo já existia em outras civilizações antes de sua formalização.  Foi Pitágoras quem formalizou a teoria com a relação geométrica, tornando-se, assim, o responsável pela sua propagação (Cerqueira, 2023).

O teorema de Pitágoras vai além da matemática pura, é aplicado em várias situações diárias do cotidiano. Por exemplo, construção de rampa de acesso, por engenheiros, precisam utilizam o teorema para garantir uma inclinação segura e adequada. O mesmo ocorre com navegações, o teorema é utilizado para determinar a distância entre dois pontos. Compreender o teorema, significa solucionar problemas de forma eficiente e objetiva, configurando a relevância prática e teórica deste (Asth, 2021)

Segundo Rabelo (2021), o teorema de Pitágoras é aplicável em diversas áreas, onde existe a necessidade de calcular distâncias. Compreender essa fórmula é essencial para vários campos da ciência e tecnologia, perfazendo base sólida para estudos futuros. A demonstração visual do Teorema de Pitágoras é a mais comum. Contudo, é possível a construção de quadrado sobre cada lado do triângulo retângulo, sendo comparada a soma das áreas dos quadrados sobre os catetos, com a área do quadrado sobre a hipotenusa. Contudo, veem-se algumas características do Teorema de Pitágoras:

• O teorema de Pitágoras aplica-se a triângulos retângulos.
• A fórmula é expressa como a² = b² + c².
• Permite calcular a medida de um lado quando os outros dois são conhecidos. 

Figura 1 – Representação do Teorema de Pitágoras

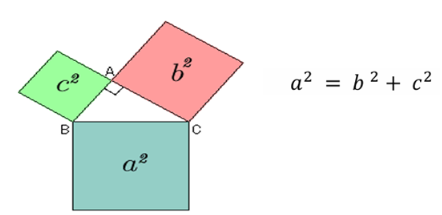
Fonte: Problema: Repensando o Teorema de Pitágoras. Disponível em:  http://clubes.obmep.org.br/blog/probleminha-repensando-o-teorema-de-pitagoras. Acesso em: 09 de maio de 2025. 

A figura acima do Teorema de Pitágoras é exemplificada por um triângulo retângulo ABC. Os triângulos possuem um ângulo de 90 graus, com o lado oposto ao ângulo reto, chamado de hipotenusa, significa o lado maior do triângulo retângulo, e os demais lados são chamados de catetos, são os lados menores do triângulo retângulo (Magalhães, 2020).

Contudo, demonstra a relação entre os comprimentos dos lados de um triângulo retângulo. Lembrando que um triângulo retângulo é uma figura geométrica composta por três lados, com um ângulo interno reto, ou seja, um ângulo de 90 graus, e os demais ângulos agudos são menores que 90 graus. A soma dos ângulos internos é igual a 180 graus, o lado maior e fica oposto ao ângulo reto, chamado de hipotenusa e os outros lados menores do triângulo são chamados de catetos (Paiva, 2021). 

Na área de arquitetura, garante que as estruturas sejam formadas por ângulos determinados e sejam seguras. Na área da computação gráfica, o teorema é aplicado para determinar distâncias entre pontos em espaço tridimensional, com a criação de gráficos e animações. Essas práticas demonstram a importância do teorema de Pitágoras em problemas reais (Tomaz, 2019). 

A resolução de problemas utilizando o teorema de Pitágoras desenvolve habilidades de raciocínio lógico e matemática dos alunos, importantes para o crescimento acadêmico e profissional. É importante que os alunos pratiquem variações de problemas para fortalecer essas habilidades e se tornem eficientes quando necessitarem aplicar o teorema de Pitágoras em diversas áreas e situações. 

NÚMEROS FIGURADOS

Ao tratar dos números figurados, estes adquiriram avanços a partir dos antigos gregos. Na antiga aritmética dos gregos, os matemáticos definiram propriedades aritméticas com a soma de números triangulares antecessores e números em outros planos. Um número figurado é um número demonstrado por pontos, e organizados de uma forma regular, como um triângulo ou um pentágono. Também são conhecidos e identificados como números poligonais, organizados para formar vários polígonos ou formas com três lados ou mais. Por exemplo, 10 é um número figurado, ou seja, é possível utilizar dez pontos e organizá-los para fazer um triângulo regular (Magalhães, 2023). 

Os pitagóricos, na tentativa de compreender a natureza íntima dos números, criaram os números figurados, expressos pela reunião de pontos em região geométrica. A Escola Pitagórica foi responsável por muitas de suas contribuições. A crença no misticismo dos números foi responsável por desenvolver padrões numéricos, como, números pares e ímpares, e também os números figurados (Tahan, 1972 [1965]; Mello e Souza, (1939 apud Andrade, p. 39, 2021).

Ao observar os padrões dos números figurados observa-se que, em todos os casos, o termo de primeira ordem é sempre o número um (1). Nessa relação o número um (1) era o criador. Os números figurados são sequências numéricas, formados a partir da sucessão de polígonos, ou seja, as sequências possuem formação poligonal. Número figurados também podem formar outros polígonos, como pentágonos ou hexágonos. O número pode criar um polígono regular. Os números figurados podem ser ímpares ou pares e podem variar de 1 ao maior número imaginável (Azevedo, 2022). 

Os números figurados cumprem especificações relativas à Matemática. Números figurados nos permitem examinar alguns padrões.  Se um determinado número pode ser organizado como um polígono regular de pontos, é um número figurado. Os números figurados também podem ser identificados como números poligonais tendo em vista a variedade de polígonos que podem formar (Cerqueira, 2023). Os números figurados são, principalmente, sequências de números que podem ser criados por figuras geométricas. A criação é feita mediante pequenos seixos, ou outros materiais semelhantes, dispostos na forma da figura em questão (Fossa, 2021). 

Conforme, Azevedo (2022), os pitagóricos estudaram intensivamente os números figurados, tudo é número, mas também figuras geométricas, na tentativa de unir geometria e aritmética buscando uma relação intrínseca entre a natureza. Os membros da sociedade pitagórica interpretavam os números como propriedades místicas, porém, a essência desses números sugere que são sequências numéricas formadas mediante figuras geométricas organizadas por pontos. 

 Os números figurados, formam uma infinidade de sequências numéricas, podem ter uma para cada figura geométrica, bastando, para isto, ter o número de componentes desta figura, e a dimensão escrita. Assim, podemos ter números figurados relacionados a figuras geométricas em dimensão arbitrária (Silva; Burmann, 2023). Os Pitagóricos desenvolveram, em particular, o princípio dos números figurados, onde os inteiros estão dispostos em forma de triângulos ou de outros polígonos (Silva, 2022).  Desta forma, uma possibilidade de como os pitagóricos chegaram ao teorema, foi mediante o interesse que demonstravam pelos números figurados, números expressos em conjuntos de pontos ou quadradinhos e formam configurações geométricas, como, por exemplo, triângulos e quadrados. Os pitagóricos foram os primeiros a identificar que esses números quadrados podiam ser obtidos com a soma de números ímpares (Alves, 2024). 

NÚMEROS PERFEITOS

Um número perfeito é conhecido como um número natural, e a soma dos divisores próprios, excluindo o próprio número, é igual ao próprio número. Alguns números foram identificados como números iguais à soma de seus divisores próprios, como 6 e 28.  Os números perfeitos são iguais à soma de seus divisores próprios, excluindo-o. Em outras palavras, um número perfeito é aquele que a soma dos seus divisores, excluindo-o, é igual ao próprio número. Por exemplo, o número 28 é um número perfeito, seus divisores são 1, 2, 4, 7 e 14, e 1 + 2 + 4 + 7 + 14 = 28 (Andrade, p. 33, 2021).

Foram os Pitagóricos que passaram a chamar números perfeitos os números naturais que for igual à soma de todos os seus divisores, excluindo-se desse grupo de divisores, o próprio número. Os números Pitagóricos são os números inteiros que cumprem o Teorema de Pitágoras a2 + b2 = c2. Também conhecidos como terno pitagórico, trio pitagórico ou ainda tripla pitagórica (Paiva, 2021).

O Terno Pitagórico, também denominado de Tripla Pitagórica, Trinca Pitagórica é uma sequência de três números inteiros relacionando-se com o Teorema de Pitágoras, ou seja, a²=b²+c² e com as possibilidades de construção de triângulos retângulos e seus respectivos quadrados, ou seja, números inteiros, não são números decimais e nem irracionais. Os números perfeitos provocam curiosidade até os dias atuais de muitos pesquisadores sobre o assunto. A existência ou não dos números perfeitos ímpares ainda não tem resposta concreta, mas existe, possuindo mais de 200 dígitos (Azevedo, 2022). 

O número seis, pelos Pitagóricos, era considerado como número da inteligência. Foi atribuído a Pitágoras os números perfeitos. Os Pitagóricos diziam que um número é perfeito quando ele é igual a soma de seus divisores próprios, exceto o próprio número. Então, eles entendiam que se Deus criou o mundo em seis dias, um número perfeito 1 + 2 + 3 = 6, assim, os três primeiros números perfeitos são 6, 28 e 496. Esses números são abordados a esses conceitos, para ilustrar como os trabalhos antigos com números inspiravam investigações. Os números Pitagóricos representavam o simples sob a forma de disposição de pontos no plano ou espaço (Andrade, p. 35, 2021).

Segundo Cerqueira (2023), temos: 

a) números lineares:

 ⋆ ⋆ ⋆ 3

 ⋆ ⋆ ⋆ ⋆ ⋆ 5

b) números planos triangulares:

 ⋆

 ⋆ ⋆

 ⋆ ⋆ ⋆ (6=1+2+3)

c) números planos quadrados:

 ⋆ ⋆ ⋆

 ⋆ ⋆ ⋆

 ⋆ ⋆ ⋆ (9=4+5)

d) números planos pentagonais:

                         ⋆

                      ⋆    ⋆

                  ⋆  ⋆    ⋆  ⋆

                     ⋆        ⋆

                     ⋆   ⋆   ⋆ (12=1+2+4+2+3)

Conforme Fossa, (2021), pode-se construir números quadrados a partir de números triangulares. Os números triangulares são considerados o conjunto dos números naturais: 1, 2, 3, 4, ···, n, ··· efetuando as somas sucessivas desses números, a partir do primeiro, e calcular os totais, assim, obtém-se: 

 1=1

 1 +2=3

 1 +2+3=6

 1 +2+3+4=10

 1 +2+3+4+5=15

· · ·

Assim, surge a sequência de resultados: 1, 3, 6, 10, 15, 21, 28, 36, ···, Estes números são os chamados de números triangulares”, interpretados pelos Pitagóricos. O quarto número triangular é o número dez. E por esse motivo o número dez para os Pitagóricos, encerrava os atributos sagrados do quatro e os atributos divinos do três (Cerqueira, 2023).

Figura 2 – Nomenclatura de Números Triangulares

Fonte: ALVES, Francisco Regis Vieira. 2024. Disponível em: https://rhmp.com.br/index.php/RHMP/article/view/119/100. Acesso em: 13 de  abril de 2025.

Segundo Silva (2022), uma fórmula específica atribuída a Pitágoras, resultava provavelmente das propriedades dos números figurados. Qualquer quadrado perfeito pode ser representado geometricamente por um conjunto quadrado de pontos, como se mostra no desenho da Figura (3) abaixo.

Figura 3- Números quadrados

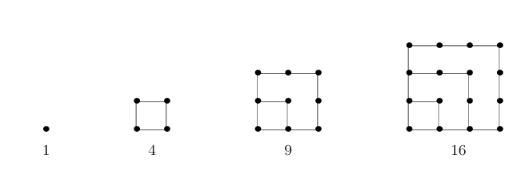
Fonte: ALVES, Francisco Regis Vieira. 2024. Disponível em: https://rhmp.com.br/index.php/RHMP/article/view/119/100. Acesso em: 13 de abril de 2025.

Esta simplicidade tinha importância para Pitágoras. A disposição triangular, chamada de adição teosófica, determina o valor secreto de um número. Assim resulta a sequência: 1, 4, 9, 16, 25, 36, 49, 64,… de números quadrados (Tomaz, 2019). Embora nem todos os historiadores da matemática compreendam que os números amigáveis e perfeitos podem ser atribuídos aos Pitagóricos, existe uma concordância universal quanto aos números figurados, que se originaram dos membros antigos da escola. Esses números, que expressam o número de pontos em certas configurações geométricas, representam um elo entre a geometria e a aritmética (Silva, 2022). 

Assim, Pitágoras buscava a perfeição numérica, onde compreendia que, “tudo é número” (Silva et al., 2016). Para Pitágoras, os divisores de um número é que irão definir a sua perfeição. Pitágoras chamava de Número Perfeito, cujos divisores somados, exceto o próprio número, dava como resultado ele mesmo. Quem se interessa pela matemática compreende o fascínio dos Pitagóricos por números e, por acreditarem que número seria o conceito fundamental, eles classificavam os números naturais de várias formas. E na busca da perfeição, os Pitagóricos criaram os números perfeitos, aqueles que se igualam à soma de suas partes (Alves, 2024). 

CONSIDERAÇÕES FINAIS

Deste modo, resta cristalino, que Pitágoras foi um filósofo e matemático grego que tinha fascínio por números e acreditava que tudo no universo poderia ter explicação mediante os números, levando-o a diversos estudos ao longo da vida, então, essa admiração pelos números, o levou a criar a Escola Pitagórica. Os seus seguidores, chamados de pitagóricos, estudavam filosofia, matemática, música e astronomia.  Foram responsáveis por propagar os ensinamentos de Pitágoras, consagradas na história e se mantém atualmente.

Resta evidente neste trabalho, o quanto Pitágoras foi uma figura importante em sua época e para os tempos atuais, tanto com relação às próprias descobertas, assim como a ideia que mesmo em tempos difíceis, sem tecnologias, contribuiu para a educação e busca por novos conhecimentos com auxílio de professores, mestres e/ou documentos antigos, como foi o caso de Pitágoras, viajando por várias regiões buscando conhecimento de outras civilizações e observando experimentos.  

Os estudos de Pitágoras referente ao teorema, serviram de impulso para a construção de sociedades melhores e, mediante esses conhecimentos, foi possível obter avanços em várias áreas do conhecimento científico. Um número perfeito é um número natural e a soma de seus divisores é igual ao número. O número em si não pode ser incluído entre os divisores. Um dos exemplos mais simples de um número perfeito é 6, pois seus divisores são: 1, 2 e 3. Se somarmos os divisores, obtemos: 1 + 2 + 3 = 6.

A construção desse trabalho contribuiu para o desenvolvimento do estudo na história, em especial do teorema de Pitágoras. O trabalho foi produzido na perspectiva de contribuir não apenas para o próprio enriquecimento intelectual e profissional, mas que sirva de auxílio para consultas, tanto de professores como de estudantes, de maneira que estes se sintam motivados e consigam desenvolver atividades educacionais sobre as relações entre a história e a aplicabilidade dos conteúdos desta ciência. 

CRONOGRAMA

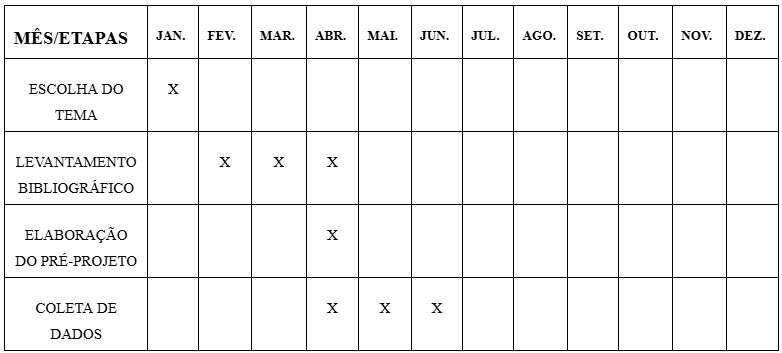
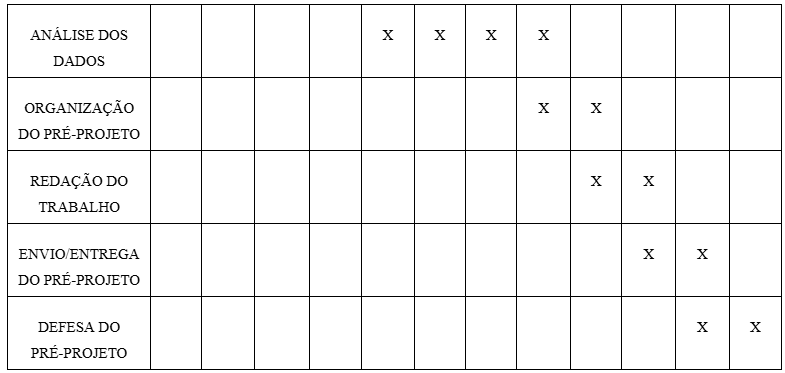
Fonte: Elaboração do autor (2025)

REFERÊNCIAS BIBLIOGRÁFICAS

ALVES, Francisco Regis Vieira. Números figurados gregos: o caso dos triangulares quadrados e sua recorrência. Revista História da Matemática para Professores, Natal (RN), v. 10, n. 1, p. 1-12, 2024. e-ISSN: 2675-715X. Disponível em: https://rhmp.com.br/index.php/RHMP/article/view/119/100. Acesso em: 09 de maio de 2025. 

ANDRADE, Filyppe Neves de. Significados produzidos a respeito de vieses entre triângulo de pascal, números tetraédricos e figurados triangulares em um processo de formação de professores de matemática. Monografia apresentada à Coordenadoria do Curso de Licenciatura em Matemática. Vitória. 2021. Disponível em: https://repositorio.ifes.edu.br/bitstream/handle/123456789/876/TCC_Significados_Produzidos_Numeros_Tetraedricos.pdf?sequence=1&isAllowed=y. Acesso em: 08 de maio de 2025. 

ASTH, Rafael C. Teorema de Pitágoras. 2021. Disponível em: https://www.significados.com.br/teorema-de-pitagoras/. Acesso em: 05 de maio de 2025. 

AZEVEDO, Luiz Felipe Araújo. Sistema permanente de avaliação do ceará: detalhamento da matriz referência de matemática do 9º ano do ensino fundamental. Dissertação apresentada ao Programa de Pós Graduação em Matemática em Rede Nacional. Fortaleza 2022. Disponível em: https://repositorio.ufc.br/handle/riufc/70252. Acesso em: 10 de maio de 2025. 

CERQUEIRA, Victor Gomes. Sobre números perfeitos e quase perfeitos. Rio de Janeiro, 2023. Dissertação apresentada, como requisito parcial para obtenção do título de Mestre. Disponível em: https://www.bdtd.uerj.br:8443/bitstream/1/23364/2/Disserta%c3%a7%c3%a3o%20-%20Victor%20Gomes%20Cerqueira%20-%202023%20-%20Completa.pdf.pdf. Acesso em: 10 de maio de 2025. 

FOSSA, John Andrew. Pitágoras, Euler, Hutton e Amigos: Ensaios sobre a História da Matemática. Primeira Edição. Natal, RN. 2021. ISBN: 978-65-00-14076-7. Disponível em: https://www.researchgate.net/profile/John-Fossa/publication/348151291_Pitagoras_Euler_Hutton_e_Amigos/links/5ff05cc3a6fdccdcb822d608/Pitagoras-Euler-Hutton-e-Amigos.pdf. Acesso em: 11 de maio de 2025. 

MAGALHÃES, Carlos Eduardo Costa. O teorema de pitágoras e algumas aplicações. Araguaína-TO. 2023. Trabalho de Conclusão de Curso apresentado ao curso de Licenciatura em Matemática. Disponível em: https://repositorio.uft.edu.br/handle/11612/4708. Acesso em: 05 de maio de 2025. 

OLIVEIRA, Elinelson Gomes de. Contando um pouco da história da trigonometria. Revista Brasileira de Ensino e Aprendizagem, v.1, p.29-58, 2021. Disponível em: https://rebena.emnuvens.com.br/revista/article/view/11/3. Acesso em: 13 de maio de 2025. 

PAIVA, Suellen Moura de. A conceituação do pensamento geométrico: aspectos históricos, filosóficos e as visões presentes em teses e dissertações no Brasil. Ilha Solteira. 2021. Dissertação apresentada junto à Faculdade de Engenharia de Ilha Solteira – UNESP. Disponível em: https://repositorio.unesp.br/server/api/core/bitstreams/9f634918-7702-4df9-b811-c31e53b941ac/content. Acesso em: 12 de maio de 2025. 

RABELO, Rigel. Teorema de Pitágoras e relações trigonométricas. 2021. Disponível em: https://blog.explicae.com.br/matematica/trigonometria-teorema-pitagoras-relacoes trigonometricas. Acesso em: 02  de maio de 2025. 

SILVA, Adelmo Luis Marques da. O estudo dos triângulos no ensino fundamental: o teorema de pitágoras e o uso do tangram. Trabalho de Conclusão de Curso em Matemática pela Universidade Federal do Pará. ACARÁ/PA. 2022. Disponível em: https://bdm.ufpa.br/server/api/core/bitstreams/1d1f8cc3-2615-4e5b-9190-c77f4738d584/content. Acesso em: 10 de maio de 2025. 

SILVA, Josivan Amorim da; BURMANN, Nilce Cruz. Relações métricas no triângulo retângulo: abordagem histórica e uma proposta de ensino utilizando-se material didático manipulável. Trabalho de Conclusão de Curso apresentado ao Instituto Federal de Alagoas. Maceió.2023. Disponível em: https://repositorio.ifal.edu.br/server/api/core/bitstreams/12ab0ee2-e895-4a8e-b97c-e95a5eb8caab/content. Acesso em: 02 de maio de 2025. 

SILVA, João Evangelista Brito da Et al. Teorema de Pitágoras: extensões e generalizações. C.Q.D. – Revista Eletrônica Paulista de Matemática, Bauru, v. 6, p. 21-47, jul. 2016. DOI: 10.21167/cqdvol6201623169664jebselcfhap2147 – Disponível em: http://www2.fc.unesp.br/revistacqd/index.jsp. Acesso em: 08 de maio de 2025.  

TOMAZ, José Roberto. O Teorema de Pitágoras: Algumas demonstrações e aplicações. O teorema de pitágoras: algumas demonstrações e aplicações. Trabalho de Conclusão de Curso apresentado ao curso de licenciatura. Campina Grande, 2019. Disponível em: https://dspace.bc.uepb.edu.br/jspui/bitstream/123456789/20980/1/PDF%20-%20Jos%c3%a9%20Roberto%20Tomaz.pdf. Acesso em: 08 de maio de 2025.